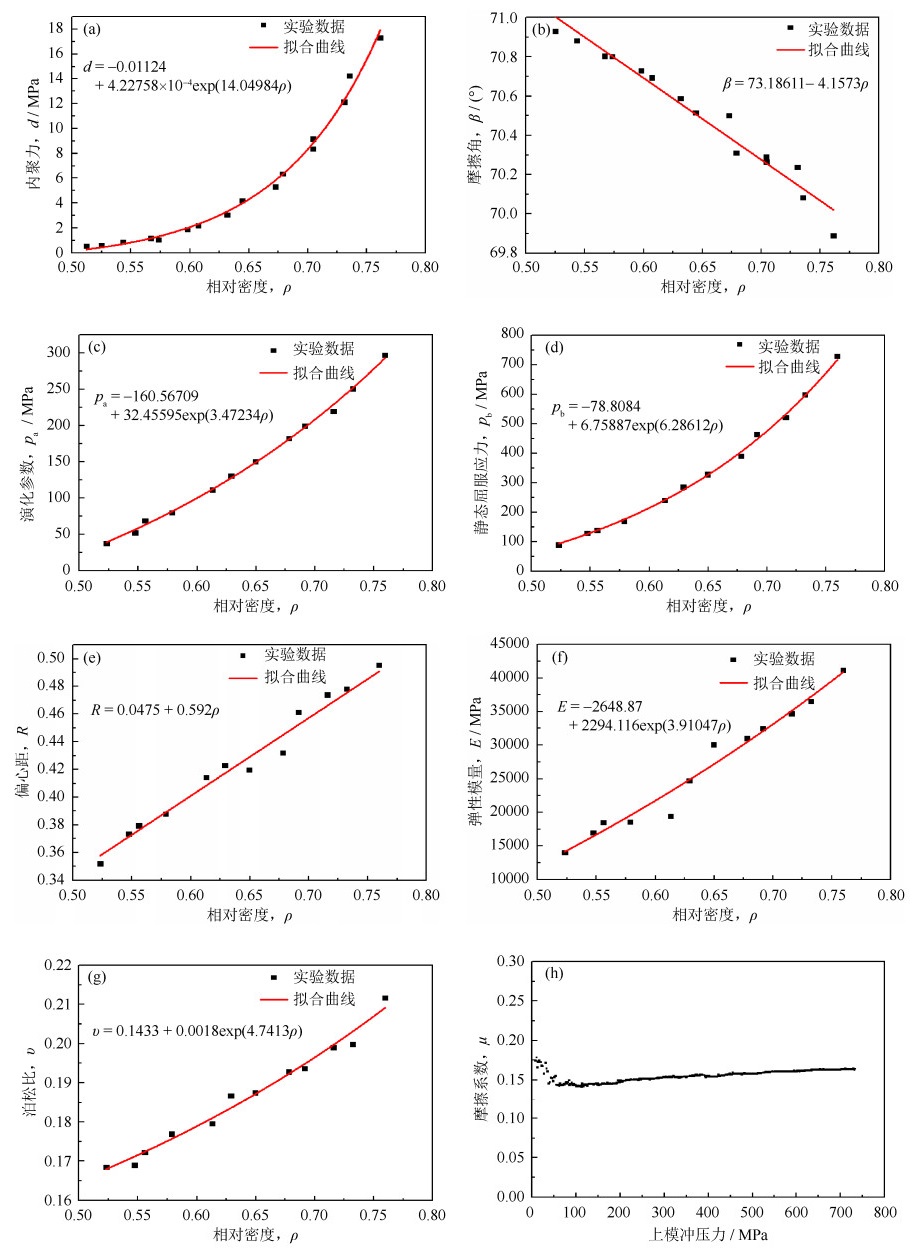
-
摘要: 通过单轴压缩实验、径向压缩（巴西圆盘）实验和冷模模压实验建立了基于密度相关修正Drucker-Prager Cap（DPC）的Ti-6Al-4V粉末压制本构模型，利用ABAQUS有限元仿真软件的二次开发用户子程序USDFLD对该本构模型进行了模拟验证。综合考虑压制过程中实验装置变形对实验数据的影响，通过空压校正实验控制实验误差，建立了更加准确的修正DPC模型。结果表明：修正DPC本构模型可很好地应用于Ti-6Al-4V粉末压制过程的仿真模拟；当上模冲压力较小时（< 50 MPa），模壁摩擦系数随上模冲压力的增加逐渐减小，当上模冲压力较大时（>50 MPa），模壁摩擦系数随上模冲压力的增加而基本趋于稳定。
-
关键词:
- Ti-6Al-4V粉末 /
- Drucker-Prager Cap模型 /
- 粉末压制 /
- 数值模拟
Abstract: The density-dependent modified Drucker-Prager Cap (DPC) constitutive model of Ti-6Al-4V powders for cold die compaction was established by uniaxial compression test, diametrical compression test (Brazilian disc experiment), and die compression test in this paper, the constitutive model was verified by the user subroutine USDFLD in secondary development based on finite element software ABAQUS. Considering the influence of device deformation on experimental data in compaction process, the experimental error was controlled by calibration experiment, and the more accurate modified DPC model was established. The results show that, the modified DPC model of Ti-6Al-4V powders for cold die compaction can be accurately used in the simulation analysis of Ti-6Al-4V powders compaction. In addition, the wall friction decreases gradually with the increase of the top punch pressure when the top punch pressure is lower than 50 MPa; while the wall friction tends to be stable with the increase of the top punch pressure, when the top punch pressure is higher than 50 MPa.-
Keywords:
- Ti-6Al-4V powders /
- Drucker-Prager Cap model /
- powder compaction /
- numerical modeling
-
铝合金是工业中应用最广泛的材料之一，因其具有高强度、高塑性、良好的抗腐蚀性等，被广泛应用在航空航天、汽车、机械制造、船舶及化学工业等领域[1–2]。其中，ZL205A合金是我国自行研制的一种高强高韧铸造合金，其强度超过了7A04、2A50等锻件和部分钢件，并具有机械加工、电镀、抗应力腐蚀等良好的综合性能，适合生产大型受力结构件，并可以用于生产以铸代锻、以铝代钢、整体铸造等构件，同时成本较低，具有较好的经济性，已在飞机、导弹、船舶、汽车等领域内大量使用[3–5]。但是，铝合金硬度较低，耐磨性较差，随着工业经济的飞速发展，对ZL205A合金材料在高速、高载荷和耐磨条件下的使用要求越来越高，为了进一步扩大铝合金的应用范围，就必须在保证其良好基体性能的基础上提高强度和耐磨性。
目前，国内普遍采用表面镀覆、表面合金化、热喷涂、激光熔覆、铸渗法、高能表面改性技术等来增强铝合金的耐磨性[6–10]，其中金属基复合材料涂层，尤其是原位颗粒增强金属基复合材料涂层，是金属耐磨材料研究的热点[11]。原位合成颗粒增强金属基复合材料技术克服了外加颗粒增强方式的缺点，具有增强颗粒尺寸小、热力学性能稳定、界面结合强度高等特点[12]。TiC和TiB2是常用的碳化物强化颗粒，具有硬度高、熔点高、热稳定性好等特点[13–14]。
自蔓延高温合成铸渗法是近年来发展起来的一种制备金属基复合材料的方法，将自蔓延高温合成（self-propagation high-temperature synthesis，SHS）技术和铸渗工艺结合，利用铸液的热量维持自蔓延反应，使金属表面原位合成复合强化涂层，从而达到强化金属基体的目的[15–16]。自蔓延高温合成铸渗法使表面合金化、表面复合与真空消失模铸渗过程同时发生，有效解决了铸渗工艺渗剂不易固定、易被金属液冲刷、涂层结合强度不高等问题。
本文将真空消失模铸造技术和自蔓延高温合成技术相结合，在铝基表面原位生成TiC和TiB2复合强化涂层，但是由于铝液浇铸温度较低，铝液经浇铸系统到达SHS粉料处时，温度不足以引燃SHS反应。因此，本文创新地在Ti–C–B4C体系中引入聚四氟乙烯（polytetrafluoroethylene，PTFE），构成Ti–C–B4C–PTFE体系，利用PTFE低温裂解成小分子气体，激发Ti–C–B4C主反应体系的SHS反应，研究ZL205A基Ti–C–B4C–PTFE体系的SHS反应和反应产物，并通过固溶处理，研究分析基体与复合涂层的热稳定。
1. 实验材料及方法
ZL205A合金是高强高韧铸造铝合金的典型代表[3]，本文以ZL205A合金为基体，其化学成分如表 1所示。通过自蔓延高温合成反应在铸件表面制备TiC–TiB2的强化涂层，采用AlCu50合金、AlMn20合金、AlTi5合金、AlCd5合金、AlV5合金和纯铝块为熔炼原料，使用钛粉、B4C粉、PTFE粉、石墨为涂层原料，其粉末粒度及纯度列于表 2；自蔓延高温合成反应体系为Ti–C–B4C–PTFE体系，利用真空消失模铸造过程中铝液传递的热量点燃反应，使体系中的Ti和C、B4C原位生成TiC和TiB2增强颗粒，通过铝液渗透作用润湿TiC–TiB2颗粒，最终形成TiC–TiB2颗粒增强铝基表面复合材料。
表 1 基体ZL205A化学成分（质量分数）Table 1. Chemical composition of ZL205A matrix% Cu Ti Cd Mn V Al 4.72 0.20 0.22 0.40 0.10 余量 表 2 涂层原料粉末粒度、纯度和成分质量分数Table 2. Particle size, purity, and mass fraction of coating material powders元素 粒度/ μm 纯度/ % 质量分数/ % Ti ~45 ≥99.7 72.6 B4C ~5 ≥99.0 19.5 PTFE ~10 ≥99.0 4.0 C ~10 ≥99.5 4.1 具体实验过程为：（1）利用加热电阻丝切割泡沫塑料，使之成为具有所需形状的模具；（2）按表 2成分配制涂层原料粉末，以球料比2:1装入球磨罐混粉1 h；（3）配制聚乙烯醇（PVA）水溶液，并与混料粉混合至膏状，然后将混合物涂覆于泡沫塑料模具表面，放入干燥箱干燥，50 ℃下干燥3 h；（4）在干燥后的泡沫塑料模上涂覆耐火涂料，放入干燥箱，在50 ℃下干燥3 h；（5）待完全干燥后，将其埋入砂箱中并用振动台振实；（6）利用中频感应炉熔炼铝合金液，当熔化温度达到780 ℃时，在机械泵抽真空条件下负压浇注；（7）5 min后将砂箱翻砂，空冷得到铸件；（8）按表 3进行固溶处理和时效处理，将铸件在马弗炉中以不同固溶温度保温10 h，在60 ℃温水中冷却，然后在干燥箱中于150 ℃人工时效8 h。
表 3 热处理工艺Table 3. Heat treatment process试样编号 固溶处理 时效处理 固溶温度/ ℃ 保温时间/ h 冷却介质 冷却温度/ ℃ 时效温度/ ℃ 保温时间/ h 冷却介质 0 铸态，不经固溶处理 1 518 10 水 60 150 8 空气 2 528 10 水 60 150 8 空气 3 538 10 水 60 150 8 空气 4 548 10 水 60 150 8 空气 利用DHB-3000型布氏硬度计测试样品的布氏硬度（压头为硬质合金球，载荷2.452 kN，加载时间30 s），并取3点平均值。采用剪切法（YS/T485-2005）表征涂层与基体之间的界面结合强度。通过ML-100型鞘盘回转式磨粒磨损试验机进行SHS涂层与基体的磨损性能测试。使用日本理学Dmax-RC型X射线衍射仪（X-ray diffraction，XRD）鉴定材料的物相组成（铜靶，λ = 0.15406 nm，管电压为40 kV，管电流为150 mA，步长0.02°，扫描速度为2°/min，测量角度范围20°~90°）。利用LEO-1450扫描电镜（scanning electron microscope，SEM）观察试样的显微组织，并用自带能谱仪（energy disperse spectroscope，EDS）定性分析涂层中各物相的化学成分。
2. 结果与讨论
2.1 SHS体系绝热温度计算
当绝热温度（Tad）大于1800 K时，自蔓延反应能够自发进行。图 1所示为Ti–C–B4C–PTFE体系绝热温度（Tad）与PTFE含量（质量分数）关系曲线，可以看出，Ti–C–B4C–PTFE体系为高放热反应体系，当PTFE的加入量在0%~15%（质量分数）时，体系的绝热温度远大于1800 K。当PTFE质量分数为4%时，体系的绝热温度为3003 K，因此自蔓延反应可自发进行。
![]()
图 1 Ti–C–B4C–PTFE体系绝热温度（Tad）与PTFE质量分数关系曲线Figure 1. Relationship between the adiabatic temperature (Tad) and PTFE content by mass in Ti–C–B4C–PTFE system2.2 X射线衍射分析
图 2所示为SHS反应前后涂层的X射线衍射图谱。可见，SHS反应前涂层中的主要物相是Ti、C和B4C，SHS反应后涂层主要由Al、TiC和TiB2相组成。可以说明，通过真空消失模技术浇注铝液时，引燃Ti–C–B4C–PTFE体系的自蔓延反应，原位生成TiC和TiB2颗粒强化相，可以有效提高铝基表面的耐磨性。在SHS过程中，Ti粉分别与B4C粉和石墨粉发生反应（4Ti+C+B4C→TiC+2TiB2），从而在铝基表面形成TiC–TiB2复合强化涂层。
2.3 硬度分析
图 3所示是热处理前后各组试样的基体和涂层显微硬度值。可以看出，铸态试样的涂层硬度值为HB 284，基体的硬度值为HB 79。经过热处理后，基体的硬度值发生明显变化，而涂层的硬度基本保持不变。当固溶温度为518 ℃时，基体的硬度提高到HB 122，此时涂层的硬度值为HB 285；当固溶温度为528 ℃时，基体的硬度从HB 79提高至HB 137，相对提高了73%；当固溶温度提高至538 ℃时，基体的硬度开始下降。可见，TiC–TiB2的复合涂层的硬度值变化与热处理无关，ZL205A铝基复合涂层试样的最佳固溶温度为528 ℃。
2.4 热稳定性分析
为了进一步分析ZL205A铝基复合涂层试样的热稳定性，研究了不同固溶温度下铝基体与涂层的显微组织变化，图 4所示为热处理前后基体的显微组织形貌。从图 4（a）可以看出，灰黑色区域对应铸态的α-Al基体组织，浅灰色区域为θ（CuAl2）相及T（Al12Mn2Cu）相，主要分布在晶界处，同时基体中存在少量不连续分布的大块物质，主要为含V、Ti、Al及杂质元素的偏析相。经固溶和时效处理后，基体的显微组织明显改善，随着固溶温度的逐步提高，以θ相为主的各种晶界相出现不同程度的溶解，到528 ℃时，基本中已无连续的θ相，如图 4（c）所示。当继续提高固溶温度至538 ℃时，θ相又重新析出，从而影响基体的热稳定性。
![]()
图 4 不同固溶温度基体的显微组织：（a）未固溶处理；（b）518 ℃；（c）528 ℃；（d）538 ℃Figure 4. Microstructures of Al matrix at different solution temperatures: (a) without solution treatment; (b) 518 ℃; (c) 528 ℃; (d) 538 ℃图 5为热处理前后涂层的显微组织形貌。结合图 5（a）和表 4可以看出，浅灰色区域主要成分为Ti和C元素（点1），暗灰色区域主要成分为Ti、C和B元素（点2），结合X射线衍射图谱分析结果可知，点1和点2分别为TiC相和TiB2相。对比发现，铸态与热处理后的涂层形貌基体一致，无明显差别。可以看出，TiC–TiB2的复合强化涂层具有良好的热稳定性，其结果与图 3结果一致，随固溶温度的提高，TiC–TiB2复合强化涂层的硬度值基本保持不变。
![]()
图 5 不同固溶温度涂层的显微组织：（a）未固溶处理；（b）518 ℃；（c）528 ℃；（d）538 ℃Figure 5. Microstructures of composite coatings at different solution temperatures: (a) without solution treatment; (b) 518 ℃; (c) 528 ℃; (d) 538 ℃位置 Al Ti B C 1 — 51.97 — 48.03 2 — 44.83 26.12 29.05 从图 6（a）涂层低倍扫描电子显微形貌中可以发现，基体与涂层的结合良好。在TiC–TiB2复合涂层中存在铝基体，铝合金作为“粘结相”将涂层粘结在一起，使其呈现较好的冶金结合。在真空消失模铸造过程中，铝合金液一方面引燃Ti–C–B4C–PTFE的自蔓延反应，形成多孔的TiC–TiB2复合涂层；另一方面，铝合金液熔渗进入复合涂层，促进涂层的致密化，并保证涂层与基体的良好结合，其结合强度达到160 MPa。
![]()
图 6 2号试样基体与涂层结合的扫描电子显微形貌：（a）低倍照片；（b）高倍照片Figure 6. SEM images of sample 2 between coating and matrix: (a) low magnification; (b) high magnification2.5 耐磨性分析
对2号试样进行磨损实验，并分别施以10、15、20 N的载荷，15 min后测定质量损失，其结果如图 7所示，随着载荷的增加，质量损失增加，但涂层的质量损失量明显低于基体的质量损失量。在10 N载荷作用下，基体的损失量为200.1 mg，涂层的损失量为24.2 mg；当载荷提高至20 N时，基体的损失量为498.6 mg，涂层的损失量为49.7 mg。可以看出，ZL205A铝基体的质量损失量明显，基体的耐磨性较差，采用SHS在基体表面原位生成TiC–TiB2的复合涂层时，可以有效提高基体的耐磨性。
3. 结论
（1）当添加质量分数为4%的PTFE时，Ti–C–B4C–PTFE体系的绝热温度为3003 K，自蔓延反应可自发进行。
（2）在真空消失模铸造ZL205A铝合金过程中，铝合金液引燃Ti–C–B4C–PTFE体系的SHS反应，在基体表面原位形成TiC–TiB2的复合涂层。同时，铝合金液熔渗进入到复合涂层中，促进涂层的致密化，且涂层与基体结合良好。
（3）相比铝基体，TiC–TiB2的复合涂层的硬度值明显较高，在285 HB左右。随着固溶温度的升高，铝基体的硬度呈先升高后降低趋势，以θ相为主的晶界相先溶解后析出，最佳的固溶温度为528 ℃；TiC–TiB2的复合涂层的硬度值基本维持不变，热处理前后的涂层形貌基体一致，说明TiC–TiB2的复合涂层具有良好的热稳定性。
（4）通过在ZL205A铝合金表面原位生成TiC–TiB2的复合涂层，大大提高了铝合金表面的耐磨性。在20 N载荷的作用下，基体的质量损失量为498.6 mg，而涂层的损失量为49.7 mg，损失量相对减少了90%。
-
![]()
图 1 压坯压缩强度测量实验：（a）单轴压缩实验；（b）巴西圆盘实验
Figure 1. Compression strength tests of the powder compacts: (a) uniaxial compression test; (b) diametrical compression test
![]()
图 3 修正DPC模型及模压实验加载路径
Figure 3. Modified DPC model and the loading path of die compaction test
![]()
图 4 剪切破坏面确定实验：（1）单轴拉伸实验；（2）剪切实验；（3）巴西圆盘实验；（4）单轴压缩实验
Figure 4. Determination of shear failure surface: (1) uniaxial tension test; (2) pure shear test; (3) diametrical compression test; (4) uniaxial compression test
![]()
图 5 压坯压缩强度与相对密度关系：（a）单轴压缩强度；（b）径向压缩强度
Figure 5. Compression strength change with relative density of powder compacts: (a) axial compression strength; (b) radial tensile strength
![]()
图 6 空压校正实验：（a）整个模压装置的力–位移曲线；（b）模压实验原始数据与修正数据的力–位移曲线
Figure 6. Die compaction tests without powders: (a) force–displacement response of the whole testing system; (b) force–displacement curves with the raw and corrected data for powder compact
![]()
图 7 修正DPC模型参数、弹性参数与相对密度的关系以及摩擦系数与上模冲压力的关系：（a）内聚力，d；（b）摩擦角，β；（c）演化参数，pa；（d）静态屈服应力，pb；（e）偏心距，R；（f）弹性模量，E；（g）泊松比，υ；（h）摩擦系数，μ
Figure 7. Relationship of modified DPC model parameters, elastic properties, and relative density and the variation of friction coefficient with top punch pressure: (a) cohesion, d; (b) friction angle, β; (c) evolution parameter, pa; (d) hydrostatic yield stress, pb; (e) cap excentricity, R; (f) Young's modulus, E; (g) Poisson's ratio, υ; (h) friction coefficient, μ
![]()
图 8 有限元模型及模拟实验：（a）组装模型；（b）划分网格模型；（c）加载完毕模型；（d）卸载完毕模型
Figure 8. Finite element model and simulation experiment: (a) assembled model; (b) model with meshes; (c) model after loading; (d) model after unloading
![]()
图 9 生坯相对密度分布云图：（a）加载完毕；（b）卸载完毕
Figure 9. Relative density distribution of green: (a) after loading; (b) after unloading
表 1 Ti–6Al–4V粉末化学成分表（质量分数）
Table 1 Chemical composition of Ti–6Al–4V powders
% Al V Fe C N H O Ti 6.00 3.90 0.05 0.02 0.180 0.039 0.20 余量 
下载: 导出CSV
-
[1] Wei W H, Wang L Z, Chen T, et al. Study on the flow properties of Ti–6Al–4V powders prepared by radio-frequency plasma spheroidization. Adv Powder Technol, 2017, 28(9): 2431 DOI: 10.1016/j.apt.2017.06.025
[2] 刘超, 孔祥吉, 吴胜文, 等. 钛及钛合金金属粉末注射成形技术的研究进展. 粉末冶金技术, 2017, 35(2): 150 DOI: 10.3969/j.issn.1001-3784.2017.02.012 Liu C, Kong X J, Wu S W, et al. Research progress on metal injection molding of titanium and titanium alloys. Powder Metall Technol, 2017, 35(2): 150 DOI: 10.3969/j.issn.1001-3784.2017.02.012
[3] 黄蓓. 基于钛合金的难加工材料切削加工工艺研究[学位论文]. 南京: 南京理工大学, 2015 Huang B. Research on Difficult-to-Cut Materials Processing Technology Based on Titanium [Dissertation]. Nanjing: Nanjing University of Science and Technology, 2015
[4] 王海英, 郭志猛, 芦博欣, 等. 钛合金粉末冶金工业化生产技术. 钛工业进展, 2017, 34(1): 1 https://www.cnki.com.cn/Article/CJFDTOTAL-TGYJ201701001.htm Wang H Y, Guo Z M, Lu B X, et al. Industrialized production technology of powder metallurgy (PM) titanium and titanium alloy. Titanium Ind Prog, 2017, 34(1): 1 https://www.cnki.com.cn/Article/CJFDTOTAL-TGYJ201701001.htm
[5] 汪俊, 李从心, 阮雪榆. 粉末金属压制过程数值模拟建模方法. 机械科学与技术, 2000, 19(3): 436 DOI: 10.3321/j.issn:1003-8728.2000.03.034 Wang J, Li C X, Ruan X Y. Modeling approach for numerical simulation of powdered metal compacting process. Mech Sci Technol, 2000, 19(3): 436 DOI: 10.3321/j.issn:1003-8728.2000.03.034
[6] Biswas K. Comparison of various plasticity models for metal powder compaction processes. J Mater Process Technol, 2005, 166(1): 107 DOI: 10.1016/j.jmatprotec.2004.08.006
[7] Bierwisch C, Kraft T, Riedel H, et al. Die filling optimization using three-dimensional discrete element modeling. Powder Technol, 2009, 196(2): 169 DOI: 10.1016/j.powtec.2009.07.018
[8] 颜士伟, 黄尚宇, 胡建华, 等. 数值仿真技术在粉末冶金零件制造中的应用及研究进展. 粉末冶金技术, 2017, 35(1): 57 DOI: 10.3969/j.issn.1001-3784.2017.01.010 Yan S W, Huang S Y, Hu J H, et al. Development and application of numerical simulation in powder metallurgy manufacturing. Powder Metall Technol, 2017, 35(1): 57 DOI: 10.3969/j.issn.1001-3784.2017.01.010
[9] Drucker D C, Gibson R E, Henkel D J. Soil mechanics and work hardening theories of plasticity. Am Soc Civ Eng, 1957, 122: 338 DOI: 10.1061/TACEAT.0007430
[10] Sinka I C, Cunningham J C, Zavaliangos A. The effect of wall friction in the compaction of pharmaceutical tablets with curved faces: a validation study of the Drucker–Prager Cap model. Powder Technol, 2003, 133(1-3): 33 DOI: 10.1016/S0032-5910(03)00094-9
[11] Reiterer M, Kraft T, Janosovits U, et al. Finite element simulation of cold isostatic pressing and sintering of SiC components. Ceram Int, 2004, 30(2): 177 DOI: 10.1016/S0272-8842(03)00086-5
[12] Zhang B S, Jain M, Zhao C H, et al. Experimental calibration of density-dependent modified Drucker–Prager/Cap model using an instrumented cubic die for powder compact. Powder Technol, 2010, 204(1): 27 DOI: 10.1016/j.powtec.2010.07.003
[13] 胡建召, 李达人, 周冰, 等. 基于Drucker–Prager/Cap模型的W–Cu20粉末轧制数值模拟. 粉末冶金技术, 2017, 35(4): 249 DOI: 10.19591/j.cnki.cn11-1974/tf.2017.04.002 Hu J Z, Li D R, Zhou B, et al. Study on numerical simulation of W–Cu20 powder rolling based on Drucker–Prager/Cap model. Powder Metall Technol, 2017, 35(4): 249 DOI: 10.19591/j.cnki.cn11-1974/tf.2017.04.002
[14] Zhou M C, Huang S Y, Hu J H, et al. A density-dependent modified Drucker–Prager Cap model for die compaction of Ag57.6–Cu22.4–Sn10–In10 mixed metal powders. Powder Technol, 2017, 305: 183 DOI: 10.1016/j.powtec.2016.09.061
[15] 周蕊. 粉末冶金压坯残余应力与裂纹损伤研究[学位论文]. 天津: 天津大学, 2013 Zhou R. Study on Residual Stress and Cracks Damage of Powder Metallurgy Compacts [Dissertation]. Tianjin: Tianjin University, 2013
[16] Lamarche K, Buckley D, Hartley R, et al. Assessing materials' tablet compaction properties using the Drucker–Prager Cap model. Powder Technol, 2014, 267: 208 DOI: 10.1016/j.powtec.2014.06.050
[17] Almanstötter J. A modified Drucker–Prager Cap model for finite element simulation of doped tungsten powder compaction. Int J Refract Met Hard Mater, 2015, 50: 290 DOI: 10.1016/j.ijrmhm.2015.02.005
[18] Han L H, Elliott J A, Bentham A C, et al. A modified Drucker–Prager Cap model for die compaction simulation of pharmaceutical powders. Int J Solids Struct, 2008, 45(10): 3088 DOI: 10.1016/j.ijsolstr.2008.01.024
[19] Zhou M C, Huang S Y, Hu J H, et al. Experiment and finite element analysis of compaction densification mechanism of Ag–Cu–Sn–In mixed metal powder. Powder Technol, 2017, 313: 68 DOI: 10.1016/j.powtec.2017.03.015
-
期刊类型引用(2)
1. 卫佳乐，白亚平，刘萌萌，李建平. 自生TiB_2-TiC_x/7075Al基复合材料显微组织与力学性能研究. 西安工业大学学报. 2022(03): 276-284 . 
百度学术
2. 谢刚，俞小花，彭如振，王有维. 大气等离子喷涂TiB_2涂层微观结构及性能研究. 轻金属. 2020(08): 27-31 . 百度学术
其他类型引用(2)
计量
- 文章访问数: 551
- HTML全文浏览量: 215
- PDF下载量: 56
- 被引次数: 4
