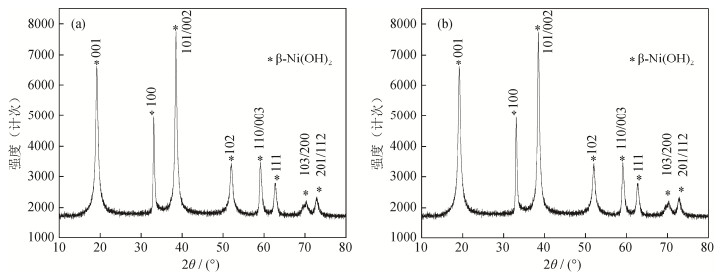
Abstract: The principle, characteristics, and equipment of microwave drying were introduced in this paper. Compared with the traditional drying technology, the advantages of microwave drying used in the precursor preparation of lithium-ion battery materials were studied and analyzed. In the results, the content of magnetic foreign body by mass introduced into the precursor of lithium ion battery material dried by microwave is greatly reduced, the dispersibility is good, and there is no agglomeration phenomenon. Compared with the traditional drying technology, there is no significant difference in phase composition of precursor dried by microwave using X-ray diffraction. The drying efficiency is improved, and the primary yield is significantly increased. Problems in the production of lithium-ion battery materials can be solved by microwave drying technology, such as the introduction of magnetic foreign body, the nonuniform drying, the poor dispersibility, and the aggregation effect, which will benefit the industrial production of lithium-ion battery materials.