Property characterization of Mn-Si powder porous alloy for semiconductors prepared by solid phase sintering
-
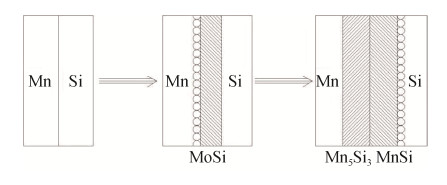
摘要: 以高纯Si粉和Mn粉为原料, 利用固相烧结技术制备得到Mn-Si粉末多孔合金, 对其组织结构及性能进行表征, 分析烧结过程中孔隙形成机理。结果表明: 600℃烧结温度可得到MnSi粉末, 烧结温度升高到1000℃后, 原有的Si与MnSi衍射峰已全部消失, 烧结体中只剩下Mn5Si3物相成分; 烧结体膨胀率和孔隙率都随烧结温度的增加表现出先增加后减小的变化规律, 在烧结温度800℃时取得最大值, 分别为8.86%和54.26%;在Mn颗粒和MnSi相之间存在明显空隙, 随着Si与Mn元素之间扩散的继续, 空隙持续增大进而连通形成层状, 随着烧结温度增加到1000℃, Mn、Si、MnSi被消耗殆尽, 合金中形成Mn5Si3结构。Abstract: The Mn-Si powder porous alloys were prepared by solid phase sintering, using high purity Si powders and Mn powders as the raw materials. The microstructure and properties of Mn-Si powder porous alloys were characterized and the for mation mechanism of pores in sintering process was analyzed. The results show that, the MnSi powders can be obtained at 600℃, with the increase of sintering temperature to 1000℃, the original diffraction peaks of Si and MnSi disappear, only Mn5Si3 phase is present inthe sintered body. The expansion ratio and porosity of the sintered body first increase and then decrease with the increase of sintering temperature, and show the maximum values (8.86% and 54.26%) at 800.℃ There is an obvious gap between Mn particles and MnSiphase, as the diffusion between Si and Mn continues, the gaps increase and then connect to form the lamellar structure; as the sintering temperature rises to 1000, Mn, Si, ℃ and MnSi is used up, the Mn5Si3 structure is formed.
-
Keywords:
- solid phase sintering /
- porous alloy /
- microstructure /
- property characterization
-
近年来国内外对增材制造技术的研究发展迅猛，其中金属增材制造技术作为整个增材制造体系中最为前沿和最有潜力的部分，是先进制造技术的重要发展方向[1-3]。在金属增材制造中，可用金属粉末种类少、制备成本高，限制了金属增材制造技术的进一步发展，因此，开发增材制造用金属粉末十分必要[4]。金属增材制造技术对粉末质量有严格要求，按能量源不同可将金属增材制造分为激光与电子束两大类型，其中基于粉末床的选区激光熔化技术要求粉末粒径在15~53 μm，并具有较高的球形度与低氧含量。在金属粉末的主要制备方法中，紧耦合气雾化技术由于导液管与气流距离最近，气体动能在飞行过程中损耗小，所制备的金属粉末具有粒度小、球形度高、成本低等优点，现已成为制备选区激光熔化用金属粉末的主流技术[5-9]。本文使用紧耦合气雾化制粉装置，研制选区激光熔化用18Ni300合金粉末，并重点揭示了雾化压力这一显性工艺参数对粉末粒度(中值粒径，D50)、粒度分布、球形度、氧含量(质量分数)、流动性和松装密度的影响规律，为选区激光熔化用18Ni300合金粉末的制备提供实际工艺指导。
1. 实验材料及方法
实验采用真空惰性气雾化设备(vacuum inert gas atomization, VIGA)，雾化气体为99.999%高纯氮气。实验原料为18Ni300合金棒料，其化学成分如表 1所示。
表 1 18Ni300合金化学成分(质量分数)Table 1. Chemical composition of the 18Ni300 alloy% Ni Mo Co Ti Mn C S P O N H 18.01 4.94 9.01 0.74 0.012 0.001 0.001 0.005 0.0005 0.001 0.00004 实验使用VIGA中频感应炉进行真空熔炼，通过红外线测温仪测量金属熔体温度。待棒料熔化并达到工艺要求温度后，向雾化炉充入氮气作为保护气体，将金属熔体倒入中间包，开启高压气阀开始雾化，具体气雾化工艺参数如表 2所示。
表 2 气雾化工艺参数Table 2. Process parameters of the gas atomization工艺 金属熔体温度/℃ 雾化压力/MPa 1 1650 ± 20 3.5 2 1650 ± 20 4.0 3 1650 ± 20 4.5 4 1650 ± 20 5.0 雾化结束后，根据GB/T 5314-2011《粉末冶金用粉末取样方法》对所制备金属粉末进行取样[10]，然后通过超声波旋振筛进行筛分，使用气流分级机去除15 μm以下粉末，统计分级质量。将粒度为15~53 μm的粉末总质量占80目筛网筛分后粉末总质量的比值作为粉末收得率(η)。
采用TESCAN VEGA3扫描电子显微镜(scanning electron microscope, SEM) 对粉末球形度、表面形貌及粒度进行观察；利用珠海欧美克LS-POP(9) 型激光粒度分析仪对粉末粒度进行分析，分散剂为去离子水；以Q=ds/dy[11]来计算和表征颗粒平均球形度(Q)，其中ds为粉末颗粒表面积等效直径，dy为颗粒体积等效直径；通过TC306氧氮分析仪对金属粉末氧含量(质量分数) 进行分析；根据GB/T 1482-2010《金属粉末流动性的测定标准漏斗法(霍尔流速计) 》和GB/T 1479.1-2011《金属粉末松装密度的测定第1部分：漏斗法》测定粉末流动性与松装密度[12-13]。
2. 结果与分析
2.1 粉末粒度
使用80目筛网对取样粉末进行筛分，并通过激光粒度仪进行粒度分析，所得18Ni300合金粉末粒径累积分布如图 1所示，不同工艺制得的粉末粒度(D50) 与收得率(η) 如表 3所示。对比工艺1、2和3可知，粉末粒度累积分布曲线随着雾化压力的增大向左偏移，其中，当雾化压力从3.5 MPa分别增加到4.0 MPa和4.5 MPa时，粉末中值粒径从60.0 μm分别减小到36.5 μm和34.0 μm，收得率η从28.5%分别增大到32.5%和38.1%。当雾化压力进一步增大至5.0 MPa(工艺4) 时，粉末粒度累积分布曲线向右偏移，粉末粒径增大且收得率降低。
![]()
图 1 不同雾化压力制备的粉末粒径累积分布Figure 1. Cumulative distribution of the powder size prepared at the different gas pressures表 3 不同工艺制备的粉末粒径(D50) 与收得率(η)Table 3. Particle size (D50) and yield (η) of the powders prepared by the different processes工艺 D50/μm η/% 1 60.0 28.5 2 36.5 32.5 3 34.0 38.1 4 40.0 35.9 这是因为雾化压力的改变将引起雾化器出口处气体速度与气体质量流率的改变，进而改变合金粉末粒度。典型的雾化过程分为两次破碎，一次破碎是金属熔体与雾化气壁接触后，发生剧烈的动量与热量交换，金属熔体破碎形成大液滴的过程，在一次破碎中，雾化压力越大，金属熔体与气流的能量交换越强，破碎而成的金属液滴越小；一次破碎后的金属液滴在气流作用下继续加速，加速后液滴表面张力增加导致破碎为更加细小的液滴，这被称作二次破碎[14-15]。在工艺1、2和3中，随着雾化压力的增大，雾化气体速度增加，动能增大，气体对18Ni300金属熔体的击打力增加，熔体更容易破碎为细小的金属液滴，并在冷却后形成小粒度金属粉末，因此粉末的中值粒径D50下降，收得率增加。在工艺4中，随着雾化压力继续增大，高速氮气气流的冲击力进一步提高，由18Ni300金属熔体破碎而成的熔融小液滴动能增加，在液滴还未冷却成球形粉末之前，更加激烈的碰撞导致小液滴之间相互融合并冷却形成粒径较大的粉末，造成平均粒径增大。此外，当尺寸差异较大的金属熔体液滴相遇时，小尺寸金属液滴冷却较快，所形成的细小金属颗粒嵌入、粘连在大粒径金属液滴表面，待大粒径液滴冷却后形成卫星球，这也造成粉末粒径的增加，收得率下降。
2.2 粉末形貌与性能
图 2为不同工艺下18Ni300合金粉末显微形貌。由图可知，工艺1所制备的金属粉末大部分为球形，但颗粒粒度分布不均，有较多大粒径颗粒及近球形颗粒；在工艺2和工艺3中，所制备金属粉末的大粒径颗粒数目减小，颗粒粒度分布均匀，粉末球形度好，不规则颗粒与近球形颗粒少，但有一定的卫星球存在，其中工艺3制备粉末球形度最高；工艺4中18Ni300合金粉末粒度增大，卫星球数目增加，有不规则粉末。
![]()
图 2 不同工艺制得的粉末形貌：(a) 工艺1; (b) 工艺2; (c) 工艺3; (d) 工艺4Figure 2. Morphology of the powders prepared by the different processes: (a) process 1; (b) process 2; (c) process 3; (d) process 4不同雾化工艺制备的18Ni300合金粉末球形度、流动性、松装密度如表 4所示。由表可知，工艺1和工艺2制备的粉末球形度低、流动性差，松装密度较小；工艺3和工艺4流动性好、松装密度大，其中工艺3制备粉末球形度最高、流动性最好，松装密度最大。
表 4 不同工艺制备粉末的球形度、流动性与松装密度Table 4. Spherical, flowability, and apparent density of the powders prepared by the different processes工艺 球形度 流动性/[s·(50 g) -1] 松装密度/(g·cm-3) 1 0.65 22.3 4.08 2 0.70 19.5 4.21 3 0.77 17.4 4.32 4 0.72 18.6 4.30 雾化压力的增加导致粉末形貌、流动性和松装密度发生变化，主要原因是金属熔体破碎后的液滴大小不同，导致粉末凝固时间及飞行速度不同。See和Johnson[16]研究得到了熔化潜热与液滴凝固时间关系经验公式，如式(1) 所示。
$$ t_{\mathrm{sol}}=\frac{d \rho_{1}}{6 h_{\mathrm{c}}}\left[c_{\mathrm{p}} \ln \left(\frac{T_{1}-T_{\mathrm{g}}}{T_{\mathrm{m}}-T_{\mathrm{g}}}\right)+\frac{\Delta H}{\left(T_{\mathrm{m}}-T_{\mathrm{g}}\right)}\right] $$ (1) 式中：tsol是液滴总凝固时间，s; d为粉末粒径，m；ρl为熔体密度，kg·cm-3; hc为传热系数，W·(m2·K) -1; cp为熔体比热容，J·kg-1·K-1; Tl、Tg、Tm分别为熔体熔化温度、雾化气体温度和金属熔点，K; ΔH为金属熔化潜热，J·kg-1。
由式(1) 可知，在金属熔体温度不变的情况下，大尺寸液滴凝固时间比小尺寸液滴长；此外，在气流场中，大尺寸液滴质量大、加速慢，飞行速度比小尺寸液滴慢。因此，在液滴飞行过程中，凝固时间、飞行速度不同的液滴在碰撞后形成了不同形貌粉末。未凝固的液滴相互碰撞融合为更大的液滴；凝固的小液滴与未凝固的大液滴碰撞，会以全包覆、嵌入、粘结等形态结合，其中嵌入与粘结状态的液滴在凝固后形成卫星球。
在工艺1、2和3中，随着雾化压力增大，气体动能转化为金属熔体表面能，金属熔体被破碎为更小的金属液滴，小液滴的表面能增大、球化时间减小；虽然凝固时间也减小了，但球化时间小于凝固时间，因此工艺3所制备的18Ni300合金粉末粒度球形度高，流动性好，松装密度大。在工艺4中，雾化压力继续增大，破碎后的小液滴数量更多，凝固后的细小粉末在气流中速度更快，细小粉末通过冲击与大尺寸金属液滴相互碰撞的概率随之增大，形成更多卫星球，卫星球的增加降低了粉末的球形度，使流动性变差，松装密度减小。
2.3 粉末氧含量(质量分数)
对四种工艺制备的18Ni300合金粉末进行取样，分别选取等质量a、b两组样品，a组为53~180 μm粉末，b组为15~53 μm粉末，使用氧氮分析仪测量N元素与O元素含量(质量分数)，检测结果如图 3所示。将四种不同工艺、同种工艺不同粉末粒度的N、O含量与18Ni300棒料进行对比，发现随着雾化压力的增大，N、O含量增加，其中N含量增幅较大；此外，15~53 μm粉末的N、O含量比53~180 μm粉末要高。这是因为较高的雾化压力将金属熔体破碎为更细小的熔滴，冷却凝固得到的粉末更细密，比表面积更大，会吸附更多的游离N、O。
![]()
图 3 不同雾化压力下粉末氧、氮含量(质量分数)Figure 3. Oxygen and nitrogen mass fractions of the powders prepared by the different processes四种雾化工艺制备的18Ni300合金粉末都能够满足选区激光熔化用金属粉末的低氧含量的要求。但使用氮气雾化制备18Ni300合金粉末，粉末中N含量将高于棒料，这将会对选区激光熔化制件的力学性能造成不利影响。可更换氩气作为雾化气体，减少N元素的引入，或通过真空脱气降低粉末的N含量。
3. 结论
(1) 在熔体温度为(1650±20) ℃、雾化压力为4.5 MPa条件下制备的18Ni300合金粉末可获得最高粉末收得率，所制备粉末球形度高，流动性好，松装密度高，满足选区激光熔化需求。
(2) 在紧耦合气雾化技术中，雾化压力的变化会导致18Ni300合金粉末粒径、表面形貌改变。在一定范围内，雾化压力增大，粉末粒径变小，球形度变好；但过高的雾化压力会导致卫星球数目增加，增大粉末粒径，降低球形度。
(3) 采用真空熔炼紧耦合气雾化技术所制备的18Ni300合金粉末O含量低，能够满足选区激光熔化要求，但粉末N元素含量较高，建议对粉末进行脱气处理或使用氩气作为雾化介质雾化。
-
![]()
图 1 不同烧结温度下Mn–Si粉末多孔合金压坯试样X射线衍射图谱
Figure 1. XRD spectra of Mn–Si powder porous alloy at different sintering temperatures
![]()
图 2 不同烧结温度下Mn–Si粉末多孔合金显微形貌：（a）400 ℃；（b）600 ℃；（c）800 ℃；（d）1000 ℃
Figure 2. SEM images of Mn–Si powder porous alloy at different sintering temperatures: (a) 400 ℃; (b) 600 ℃; (c) 800 ℃; (d) 1000 ℃
![]()
图 3 不同烧结温度下Mn–Si粉末多孔合金孔隙显微形貌：（a）600 ℃；（b）1000 ℃
Figure 3. Pore morphology of Mn–Si powder porous alloy at different sintering temperatures: (a) 600 ℃; (b) 1000 ℃
表 1 不同烧结温度下Mn–Si粉末多孔合金的膨胀率和孔隙率
Table 1 Expansion ratio and porosity of Mn–Si powder porous alloy at different sintering temperatures
烧结温度/ ℃ 膨胀率/ % 孔隙率/ % 400 0.62 33.25 600 2.84 38.46 800 8.86 54.26 1000 5.66 51.08 
下载: 导出CSV
表 2 不同烧结温度下Mn–Si粉末多孔合金的孔径
Table 2 Pore diameters of Mn–Si powder porous alloy at different sintering temperatures
烧结温度/ ℃ 平均孔径/ μm 最大孔径/ μm 400 6.12 11.62 600 5.86 10.86 800 6.84 12.74 1000 10.26 13.85
下载: 导出CSV
-
[1] 李婷婷, 彭超群, 王日初, 等. Fe-Al、Ti-Al和Ni-Al系金属间化合物多孔材料的研究进展. 中国有色金属学报, 2011, 21(4): 784 https://www.cnki.com.cn/Article/CJFDTOTAL-ZYXZ201104013.htm Li T T, Peng C Q, Wang R C, et al. Research progress in porous Fe-Al, Ti-Al and Ni-Al intermetallic compound porous materials. Chin J Nonferrous Met, 2011, 21(4): 784 https://www.cnki.com.cn/Article/CJFDTOTAL-ZYXZ201104013.htm
[2] He Y H, Jiang Y, Xu N P, et al. Fabrication of Ti-Al micro/nanometer-sized porous alloys through the Kirkendall effect. Adv Mater, 2007, 19(16): 2102 DOI: 10.1002/adma.200602398
[3] De Boor J, Kim D S, Ao X, et al. Temperature and structure size dependence of the thermal conductivity of porous silicon. Europhys Lett, 2011, 96(1): 16001 DOI: 10.1209/0295-5075/96/16001
[4] Kanemitsu Y. Light emission from porous silicon and related materials. Phys Rep, 1995, 263(1): 1 DOI: 10.1016/0370-1573(95)00021-4
[5] Ge M, Fang X, Rong J, et al. Review of porous silicon preparation and its application for lithium-ion battery anodes. Nanotechnolog, 2013, 24(42): 422001 DOI: 10.1088/0957-4484/24/42/422001
[6] Anglin E J, Cheng L Y, Freeman W R, et al. Porous silicon in drug delivery devices and materials. Adv Drug Delivery Rev, 2008, 60(11): 1266 DOI: 10.1016/j.addr.2008.03.017
[7] Dong H X, He Y H, Zou J, et al. Effect of preheating treatment at 575℃ of green compacts on porous NiAl. J Alloys Compd, 2010, 492(1-2): 219 DOI: 10.1016/j.jallcom.2009.12.018
[8] Seitz F. On the porosity observed in the Kirkendall effect. Acta Metall, 1953, 1(3): 355 DOI: 10.1016/0001-6160(53)90112-6
[9] 倪锋, 傅丽华, 邓攀, 等. SiO2-B2O3-Al2O3助焊剂对粉末烧结Cu-C-SnO2多孔材料组织与性能的影响. 粉末冶金技术, 2018, 36(5): 335 DOI: 10.19591/j.cnki.cn11-1974/tf.2018.05.003 Ni F, Fu L H, Deng P, et al. Effects of SiO2-B2O3-Al2O3 scaling powder on microstructures and properties of Cu-C-SnO2 porous materials sintered by powders. Powder Metall Technol, 2018, 36(5): 335 DOI: 10.19591/j.cnki.cn11-1974/tf.2018.05.003
[10] 杨建明, 汤阳, 顾海, 等. 3D打印制备多孔结构的研究与应用现状. 材料导报, 2018, 32(15): 2672 DOI: 10.11896/j.issn.1005-023X.2018.15.020 Yang J M, Tang Y, Gu H, et al. Research and application of 3D printed porous geometric structure: a review. Mater Rev, 2018, 32(15): 2672 DOI: 10.11896/j.issn.1005-023X.2018.15.020
[11] 赵洋, 任淑彬, 王凤林, 等. 铜基高通量换热管内多孔层的制备及性能研究. 粉末冶金技术, 2018, 36(3): 170 DOI: 10.19591/j.cnki.cn11-1974/tf.2018.03.002 Zhao Y, Ren S B, Wang F L, et al. Preparation and properties of porous layer in copper based high flux heat transfer tube. Powder Metall Technol, 2018, 36(3): 170 DOI: 10.19591/j.cnki.cn11-1974/tf.2018.03.002
[12] 邹志欢, 曾凡浩, 刘吉安, 等. 熔渗制备B4C-MgSi复合材料的熔渗动力学、微观结构及力学性能. 粉末冶金材料科学与工程, 2018, 23(3): 252 https://www.cnki.com.cn/Article/CJFDTOTAL-FMGC201803004.htm Zou Z H, Zeng F H, Liu J A, et al. Infiltration kinetics, microstructure and mechanical properties of B4C-MgSi composite fabricated by melt infiltration. Mater Sci Eng Powder Metall, 2018, 23(3): 252 https://www.cnki.com.cn/Article/CJFDTOTAL-FMGC201803004.htm
[13] 张美丽, 解腾飞, 杨超普, 等. 尿素含量对Ti-10% Mg多孔材料孔隙结构和抗压性能的影响. 材料开发与应用, 2018, 33(2): 79 https://www.cnki.com.cn/Article/CJFDTOTAL-CLKY201802014.htm Zhang M L, Xie T F, Yang C P, et al. Effect of urea contents on pore structure and compressive properties of Ti-10% Mg porous materials. Dev Appl Mater, 2018, 33(2): 79 https://www.cnki.com.cn/Article/CJFDTOTAL-CLKY201802014.htm
[14] 付正容, 王修昌, 金青林, 等. 多孔非晶合金及其复合材料的制备技术研究进展. 材料导报, 2018, 32(2): 473 https://www.cnki.com.cn/Article/CJFDTOTAL-CLDB201803019.htm Fu Z R, Wang X C, Jin Q L, et al. A review of the preparation techniques for porous amorphous alloys and their composite. Mater Rev, 2018, 32(2): 473 https://www.cnki.com.cn/Article/CJFDTOTAL-CLDB201803019.htm
[15] 谢锐, 黄峰, 方茜, 等. 熔炼-球磨二步法制备Fe-Mn-Si三元合金. 电池, 2011, 41(3): 135 https://www.cnki.com.cn/Article/CJFDTOTAL-DACI201103004.htm Xie R, Huang F, Fang Q, et al. Preparing Fe-Mn-Si ternary alloy by melting-ball-milling two-step method. Battery Bimonthly, 2011, 41(3): 135 https://www.cnki.com.cn/Article/CJFDTOTAL-DACI201103004.htm
-
期刊类型引用(3)
1. 马亮，杨静，王继平，许奎. 粉末注射成形制备薄壁Al_2O_3–B_4C环形芯块. 粉末冶金技术. 2022(03): 211-217 . 
本站查看
2. 刘春佳，刘翔，练友运，宋久鹏，赵伟. 国际热核聚变实验堆朗缪尔探针用高纯氧化铝陶瓷的制备. 济南大学学报(自然科学版). 2021(04): 395-399+404 . 百度学术
3. 陈树群，胡海栋，周文元，胡鹏，李洪义，王金淑. 微量Fe元素对氧化钨粉还原过程的影响. 粉末冶金技术. 2021(03): 209-215 . 本站查看
其他类型引用(2)
计量
- 文章访问数: 245
- HTML全文浏览量: 60
- PDF下载量: 16
- 被引次数: 5
