Effect of loading speed on pressure distribution in metal powder pressing based on discrete element method
-
摘要: 基于离散元原理，采用三维离散元软件PFC3D模拟冲头加载过程，研究以不同冲头速度撞击金属粉末颗粒所产生的透射波以及对侧壁的压力分布。结果表明，对于离散性介质，冲击加载下的应力波传播不单受到颗粒材质波阻抗的影响，还受到颗粒运动和力链形成的很大影响。通过对比不同冲击加载速度下阴模底部的受力，发现随着冲击速度的提高，透射波的峰值成线性增长；通过均分阴模侧壁的方式得到侧壁不同位置所受的侧压力峰值，发现侧壁所受压力呈波谷式分布，从而分析得到颗粒间力链的传播和分布规律。Abstract: The punch loading process was simulated by three-dimensional discrete element software PFC3D based on discrete element method (DEM), the effects of punch loading speeds on the transmission wave of metal powders generated by the impact and the pressure distribution on the sidewall were investigated. In the results, for the discrete media, the stress wave propagation under impact loading is determined not only by the wave impedance of particle material, but also by the particle motion and force chain formation. By comparing the force on the bottom of female mold in the different loading speeds, it is found that the peak of transmission wave increases linearly with the increase of loading speed. The lateral pressure peak on different positions is obtained by means of the side wall of female mold. It is found that the pressure on the sidewalls is present as the valley-like distribution, and the propagation and distribution of the inter-particle force chains are analyzed.
-
Keywords:
- discrete element /
- impact loading /
- transmission wave /
- lateral pressure /
- stress wave
-
粉末高速压制技术[1‒4]（high velocity compaction，HVC）是一项通过高速冲击粉末来获得高致密度冶金零件的技术，其优点主要包括冲击压制速度高（通常2~30 m/s）、制品消耗成本低、成品密度高且均匀、生产效率高等。在高速压制过程中，冲头在极短时间内撞击粉末，产生应力波，应力波在传递至阴模底部后回弹，实现粉末压实，改善压坯的密度分布，提高制品密度。因此，该技术在探究粉末致密化机理，提高制品致密化以及优化加工工艺上有着显著的研究意义。
离散元法（discrete element method，DEM）[5‒7]于20世纪70年代初由Cundall首先提出，该方法将离散体视为一定数量的离散元组合，通过把每个颗粒或块体当成特定的单元体，分析某一时间段内各个颗粒之间的相互作用效果，根据牛顿运动定律的交替迭代来研究整体系统的状态。颗粒流动程序（particle flow code，PFC）可用于对颗粒流模型的力学状态进行分析，主要包括颗粒流系统的稳定、局部颗粒部分变形及本构关系。
目前，通过离散元法对粉末压制成型进行研究在国内外均取得了显著的成果：程远方等[8]利用离散元法在2D条件下模拟颗粒的随机排列以及其压制过程，分析了材料参数和压制工艺对压制密度的影响。郑州顺等[9]基于离散元法，通过颗粒流动程序软件对粉末高速压制成形过程的颗粒流动情况及密度分布进行了模拟，分析得出了阻尼系数变化对求解过程的敛散性和压坯密度分布的影响。杜欣等[10]运用不规则外形颗粒离散元建模方法进行撞击模拟和自然安息角模拟，研究颗粒外形对微观咬合摩擦和宏观咬合作用的影响。在高速压制时，冲头冲击会对粉末产生一个力的扰动，接触到表层颗粒后，扰动会通过颗粒与颗粒之间的相互挤压逐步向压坯内部传播，这种扰动的传播即为应力波。相比于常规压制，高速压制下应力波的存在是影响压坯质量的重要因素之一。曹秒艳等[11]运用离散元法模拟固体颗粒介质在单轴压缩下的受力过程，从力链的角度分析固体颗粒介质在压缩过程中细观结构的变化规律。易明军等[12]在探究力与应力波对高速压制压坯质量的影响研究中发现，应力波在自由端面反射后会造成拉应力，会导致压坯表面分层和剥落。另外，在高速冲击压制下，金属粉末颗粒之间会发生部分挤压和碰撞，颗粒产生局部变形，碰撞颗粒间接触力的传递形式也是影响金属粉末压制效果的因素。由此可知，高速压制下应力波的传播和颗粒接触对金属粉末压制效果有较大影响。
为使数值模拟更贴近于实际情况，本文基于离散元法，采用3D颗粒流动程序模型，从微观立体层面对高速压制金属粉末进行模拟分析。通过分析冲头以不同速度撞击粉末颗粒对模具侧壁产生的压力，研究颗粒间力链[13‒15]的传播规律以及冲模速度与阴模底部所受压力的关系。
1. 模型建立
建立颗粒流动程序模型的基本思想是将颗粒定义为刚体圆形（2D）或球形（3D），颗粒既不可发生变形，也不会出现破坏，且颗粒间的接触为软接触，即刚性颗粒间允许出现重叠，模型控制方程遵循牛顿第二定律，如式（1）所示。
$$ \left\{ {\begin{array}{*{20}{l}} {{m_{\rm{p}}} \cdot \mathit{\boldsymbol{g}} + \sum {{\mathit{\boldsymbol{f}}_\mathit{\boldsymbol{i}}}} = {m_{\rm{p}}} \cdot {\mathit{\boldsymbol{a}}_{\bf{p}}}}\\ {\sum {\left( {{\mathit{\boldsymbol{f}}_\mathit{\boldsymbol{i}}} \times {\mathit{\boldsymbol{r}}_\mathit{\boldsymbol{i}}}} \right)} = {I_{\rm{p}}} \cdot {\mathit{\boldsymbol{\alpha }}_{\bf{p}}}} \end{array}} \right. $$ (1) 式中：mp表示颗粒质量，g为重力加速度，fi为颗粒第i个接触力向量（i = 1，2，3，…，N），ap为颗粒质心加速度矢量，ri为颗粒第i个接触到质心的矢量，Ip表示颗粒转动惯量，αp表示颗粒转动角加速度矢量。
为了研究金属粉末在冲击加载中，加载速度对成形效果的影响以及模壁侧压力沿轴向分布的规律，建立尺寸为ϕ10 mm × 5 mm的圆柱体空间模型，初始孔隙率为0.506，采用distribute颗粒生成方式生成直径为0.15 mm的13845个圆形颗粒，在Z方向以10 m/s的速度下压加载。本次模拟步长设置为1×10-8 s，压板下行时间25×10-6 s，加载前，颗粒重排用时1000步，加载完成后运算时间忽略不计，压制过程共进行计算3500步。模拟主要参数如表 1所示。
表 1 金属粉末冲击加载模拟主要参数Table 1. Main simulation parameters of metal powder impact loading密度/(kg·m-3) 颗粒直径/mm 颗粒间摩擦系数 模壁摩擦系数 刚度系数 冲击速度/(m·s-1) 2700 0.15 0.3 0.1 108 10 模型使用是改进的软球模型，把颗粒间接触过程简化为弹簧振子的阻尼振动，其运动方程如式（2）所示。
$$m\ddot x + \eta \dot x + kx = {\rm{0}}$$ (2) 式中：x是偏离平衡位置的位移；m是振子质量；η和k分别为弹簧阻尼系数和弹性系数。模型高度为5 mm，将圆柱形侧壁分成5层，每层高度1 mm，在10 m/s的冲击速度下，测量各层模壁的受力情况。按从下到上的顺序，依次逐层生成颗粒，最底层编号为1#，最顶层编号为5#，按颗粒填充高度依次排列，如图 1所示。
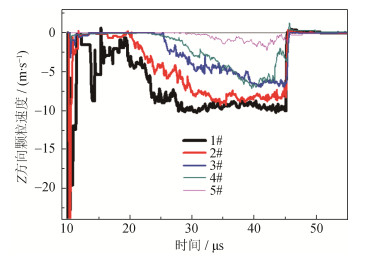
在压制过程中，颗粒在压制方向上的运动速度波形与透射波衍化波形一致，因此选取不同高度层中间位置的颗粒，记录其在压制方向上的速度波形图，如图 2所示，从上而下分别是1#、2#、3#、4#、5#层对应颗粒的速度波形图。从图中可以看出随着冲击载荷的向下传播，冲击能量会逐渐衰减，颗粒所受冲击减弱，速度降低。
2. 冲击速度对成形效果的影响
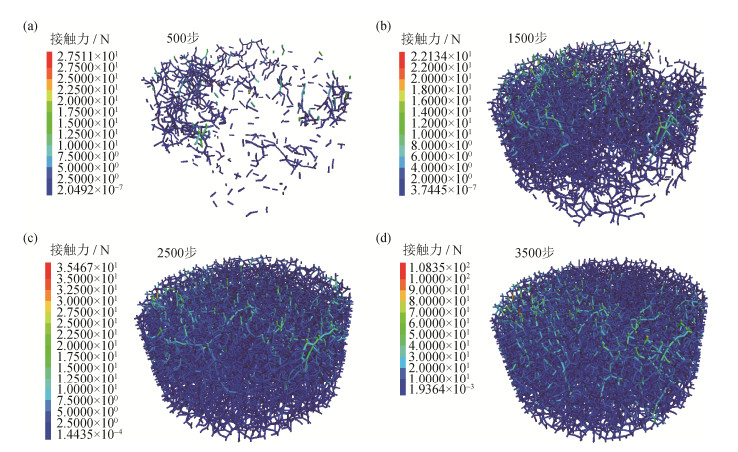
为研究撞击速度对压制效果的影响，选取5~20 m/s范围内的5组速度，研究相应的透射波波形。为保证总压制行程相同，改变每次模拟的运算时间，具体情况如表 2所示。图 3是10 m/s冲击速度下数值模拟力链生成的过程。
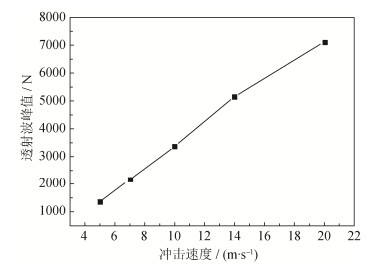
表 2 冲击速度与对应的运行时间Table 2. Impact speed and corresponding running time冲模速度/(m·s-1) 5 7 10 14 20 运行总时间/μs 70 50 35 25 17.5 ![]()
图 3 10 m·s-1冲击速度下模拟颗粒力链生成过程：（a）500步；（b）1500步；（c）2500步；（d）5300步Figure 3. Simulation process of inter-particle force chains at the impact velocity of 10 m·s-1: (a) 500 steps; (b) 1500 steps; (c) 2500 steps; (d) 3500 steps获得的5组透射波波形图如图 4所示，可以看出透射波波形基本相同，仅存在一些细微的变化。将不同速度下的加载过程均分为前期、前中期、中期、中后期和后期5个阶段，对比不同步接触力的大小，通过数值作差确定波形中出现的波峰波谷次数，分别记录各时间段内上下波动（振动）次数，统计如表 3。可以看出，随着加载速度的提升，加载期间的振动频率逐渐减少。同一速度下，随着加载时间的推移，振动次数整体呈下降趋势，且加载后期的振动明显减少。相较于加载速度为5 m/s的总振动次数（192次），7 m·s-1的总振动次数下降了33.85%，10 m/s的下降了55.21%，14 m/s的下降了73.44%，20 m/s的下降了85.42%，可以看出随着加载速度的提高，透射波传播愈加平稳。冲击加载过程中颗粒的透射波振动主要是源自颗粒重排，加载速度提高，会使颗粒加快力链网络的形成，使颗粒系统更快形成稳定的结构，削弱颗粒的运动，可能会不利于粉体间空隙的填充和空气的排除。但另一方面，随着加载速度的提升，透射波的峰值也随之呈线性增长。图 5为透射波峰值与速度的关系，可以看出，两者之间基本呈线性正相关。说明加载速度越高，金属粉末受力越大，颗粒可能发生更大的塑性变形，为压坯提供更大的机械啮合力。这一现象也证明了冲击加载与静加载的不同以及数值模型的准确性。
![]()
图 4 不同冲击加载速度对应的透射波峰值图Figure 4. Peak value of transmission wave in different impact loading speeds表 3 不同冲击加载速度和压制时段的透射波振动次数Table 3. Vibration frequency of transmission wave in different impact loading speeds at different suppression periods冲击加载速度/(m·s-1) 透射波振动次数 前期 前中期 中期 中后期 后期 5 55 50 34 30 23 7 43 35 17 21 11 10 30 20 14 15 7 14 19 12 12 6 2 20 12 9 2 4 1 ![]()
图 5 透射波峰值与冲击加载速度关系Figure 5. Relationship of transmission wave and impact loading speed在对连续性介质的高应变率加载响应的研究中，通常只研究沿压制方向的应力波情况，而忽略材料的切向变形情况。但对于非连续介质，阴模同样参与粉末材料的成形，因此阴模的受力情况以及其对成形效果的影响也是粉末冶金领域的一个研究热点。常规实验研究方法是在压坯脱模时，研究脱模力的变化情况，脱模力越小越有利于保护烧结压坯的完整性，且经实验证实，在冲击加载条件下可以获得更小的脱模力。在实验方面，可以通过采用边壁粘贴应变片等多种手段获取阴模边壁应力分布情况，本文将利用离散元三维数值模型研究沿轴向不同位置的阴模受力情况。
3. 模壁侧压力分布研究
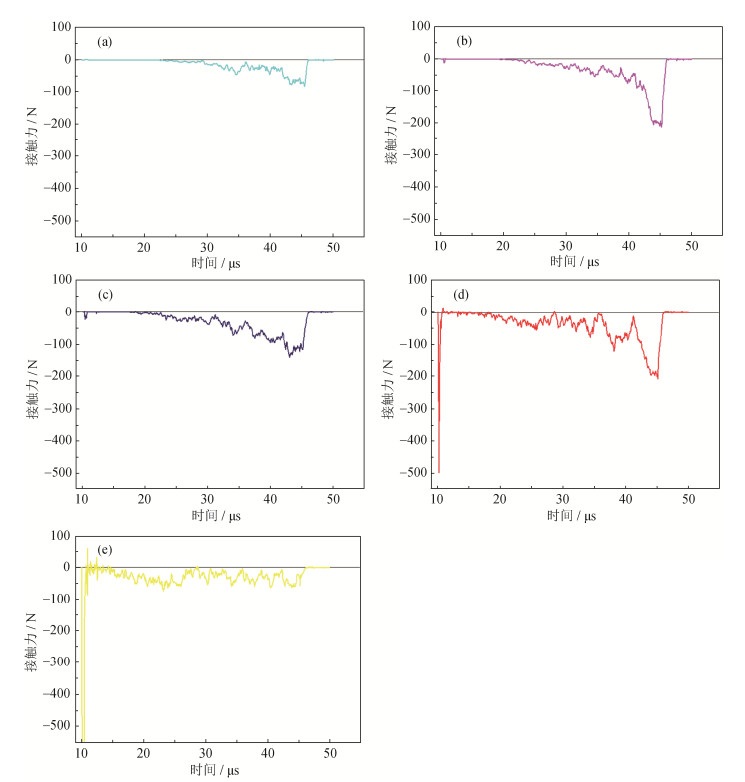
金属颗粒在10 m/s的冲击速度下，通过测量固定在各层侧壁模壁上所受力的法向分量，得到模壁受力与时间关系曲线，如图 6所示。图 6（e）对应的第5层（顶层）粉末颗粒在加载初期受力较大，但随着颗粒的下移，模壁受力接近于零；其余各层粉末颗粒的受力曲线都存在剧烈的振动，且随着压制的进行，模壁受力都逐渐增大。因为加载初期，接近顶层的颗粒会出现短暂的剧烈震动现象，所产生的侧压力幅值变化较大，不能准确反映实际压制过程中的侧壁压力，因此选取进入压制平稳阶段的最大侧压力。为研究各层模壁所受到的最大作用力分布情况，同样是在5~20 m/s冲击速度范围内，记录不同冲击速度下各层最大作用力，绘制表格如表 4所示。
![]()
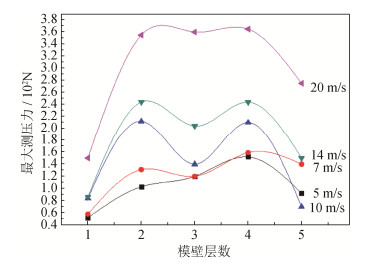
图 6 不同颗粒填充高度下模壁侧压力随时间变化情况：（a）1#；（b）2#；（c）3#；（d）4#；（e）5#Figure 6. Relationship of time and lateral pressure on die wall in different particle-filled heights: (a) 1#; (b) 2#; (c) 3#; (d) 4#; (e) 5#表 4 不同颗粒填充高度下侧压力峰值与冲击加载速度的关系Table 4. Relationship of impact loading speeds and peak values of lateral pressure on die wall in different particle-filled heights冲击速度/(m·s-1) 最大压力/(102N) 一层 二层 三层 四层 五层 5 0.52 1.03 1.20 1.52 0.92 7 0.58 1.31 1.20 1.59 1.40 10 0.84 2.12 1.40 2.10 0.70 14 0.86 2.44 2.04 2.44 1.50 20 1.50 3.55 3.60 3.65 2.75 根据表格绘制出各层所对应最大模壁受力的分布情况，如图 7所示，可以看出图形呈M状，图形中存在两个波峰，一个波谷，最底层压坯受力最小，随着加载速度的升高，侧压力峰值随之升高。图 8为数值模拟程序运行结束后的力链剖面图，其中浅色线代表强力链，深色线代表弱力链，在模型左上方可以清楚的看到一个强力链网络，并从顶板上延伸到模壁中部和左侧壁。在图中还可以看到，模型中存在两个明显的强力链网络，一个呈“树枝状”位于模型正中心，上部存在多条强力链分支，由压板向下生成，在中间部位汇聚成一条线段，在底层又分散生长出若干分支连接到底板；另一个强力链网络呈“网状”位于模型左上角，从顶板上生成延伸到模壁中部。强力链之间存在大量随机分布的弱力链，对颗粒系统的稳定起到了支撑作用。随着压制的进行，强力链逐渐向下生长，大量的弱力链在强力链周围生成，使得许多强力链会由压板中心方向向侧壁方向生长。侧壁力链的交错生长对模壁侧压力的分布产生影响，且在加载期间颗粒间的扰动以及局部颗粒的重排现象也会引起模壁侧压力的分布不均。当冲击速度小于10 m/s时，加载速度不是很快，颗粒有足够的时间进行重排、填充空隙，压力分布较为均匀，因此双峰现象会减弱，导致趋近于顶层的颗粒最大侧压力与峰值较为接近。随着加载速度的增大，颗粒与模壁之间的摩擦压力增大，使得力的损失也增加，进而阻碍了模壁侧压力的增大。
![]()
图 7 不同速度下模壁侧压力峰值与颗粒填充高度的关系Figure 7. Relationship between the peak value of lateral pressure and particle-filled height at different impact loading speeds4. 结论
利用三维颗粒离散元数值模拟软件，对金属粉末的冲击加载过程进行数值模拟，通过观察应力波透射波波形，分析冲击加载速度对成形作用的影响和模壁上侧压力的分布情况。
（1）随着加载速度的提升，加载前期的振动强度逐渐减少。说明加载速度的提高会使颗粒系统更快的形成稳定结构，因此会削弱颗粒的运动，不利于粉体间空隙的填充和空气的排除。随着加载速度的提升，透射波的峰值也随之增长，两者基本呈线性正相关。说明加载速度越高，金属粉末的受力越大，可以为压坯提供更大的机械啮合力。
（2）随颗粒填充高度的增加，模壁所受最大侧压力呈波浪式分布，可能出现多个波峰与波谷，其生成原因主要是模壁上强力链的交错排列。
（3）应用颗粒流动程序三维模型，可以准确模拟出在粉体间存在较大空隙的情况下（即粉末接近于松装的情况）的应力波透射波波形。当冲击加载速度为5 m/s时，总振动次数约为192次，7 m/s冲击速度的总振动次数相对下降了33.85%，10 m/s冲击速度的总振动次数相对下降了55.21%，14 m/s冲击速度的总振动次数相对下降了73.44%，20 m/s冲击速度的总振动次数相对下降了85.42%。说明随着模型中空隙的减少，颗粒的振动情况将减弱，透射波曲线呈阶跃式上升。
-
![]()
图 3 10 m·s-1冲击速度下模拟颗粒力链生成过程：（a）500步；（b）1500步；（c）2500步；（d）5300步
Figure 3. Simulation process of inter-particle force chains at the impact velocity of 10 m·s-1: (a) 500 steps; (b) 1500 steps; (c) 2500 steps; (d) 3500 steps
![]()
图 4 不同冲击加载速度对应的透射波峰值图
Figure 4. Peak value of transmission wave in different impact loading speeds
![]()
图 5 透射波峰值与冲击加载速度关系
Figure 5. Relationship of transmission wave and impact loading speed
![]()
图 6 不同颗粒填充高度下模壁侧压力随时间变化情况：（a）1#；（b）2#；（c）3#；（d）4#；（e）5#
Figure 6. Relationship of time and lateral pressure on die wall in different particle-filled heights: (a) 1#; (b) 2#; (c) 3#; (d) 4#; (e) 5#
![]()
图 7 不同速度下模壁侧压力峰值与颗粒填充高度的关系
Figure 7. Relationship between the peak value of lateral pressure and particle-filled height at different impact loading speeds
表 1 金属粉末冲击加载模拟主要参数
Table 1 Main simulation parameters of metal powder impact loading
密度/(kg·m-3) 颗粒直径/mm 颗粒间摩擦系数 模壁摩擦系数 刚度系数 冲击速度/(m·s-1) 2700 0.15 0.3 0.1 108 10 
下载: 导出CSV
表 2 冲击速度与对应的运行时间
Table 2 Impact speed and corresponding running time
冲模速度/(m·s-1) 5 7 10 14 20 运行总时间/μs 70 50 35 25 17.5
下载: 导出CSV
表 3 不同冲击加载速度和压制时段的透射波振动次数
Table 3 Vibration frequency of transmission wave in different impact loading speeds at different suppression periods
冲击加载速度/(m·s-1) 透射波振动次数 前期 前中期 中期 中后期 后期 5 55 50 34 30 23 7 43 35 17 21 11 10 30 20 14 15 7 14 19 12 12 6 2 20 12 9 2 4 1
下载: 导出CSV
表 4 不同颗粒填充高度下侧压力峰值与冲击加载速度的关系
Table 4 Relationship of impact loading speeds and peak values of lateral pressure on die wall in different particle-filled heights
冲击速度/(m·s-1) 最大压力/(102N) 一层 二层 三层 四层 五层 5 0.52 1.03 1.20 1.52 0.92 7 0.58 1.31 1.20 1.59 1.40 10 0.84 2.12 1.40 2.10 0.70 14 0.86 2.44 2.04 2.44 1.50 20 1.50 3.55 3.60 3.65 2.75
下载: 导出CSV
-
[1] 杨霞. 粉末冶金高速压制致密化机制的研究进展. 粉末冶金工业, 2016, 26(5): 57 https://www.cnki.com.cn/Article/CJFDTOTAL-FMYG201605019.htm Yang X. Research progress on densification mechanism of powder metallurgy highvelocity compaction. Powder Metall Ind, 2016, 26(5): 57 https://www.cnki.com.cn/Article/CJFDTOTAL-FMYG201605019.htm
[2] 王建忠, 曲选辉, 尹海清, 等. 铁粉的高速压制成形. 材料研究学报, 2008, 22(6): 589 DOI: 10.3321/j.issn:1005-3093.2008.06.006 Wang J Z, Qu X H, Yin H Q, et al. High velocity compaction of ferrous powder. Chin J Mater Res, 2008, 22(6): 589 DOI: 10.3321/j.issn:1005-3093.2008.06.006
[3] 何杰, 肖志瑜, 关航健, 等. 纯钛粉高速压制行为及其烧结性能研究. 粉末冶金技术, 2016, 34(3): 178 DOI: 10.3969/j.issn.1001-3784.2016.03.004 He J, Xiao Z Y, Guan H J, et al. High velocity compaction behavior and sintered properties of pure Ti powder. Powder Metall Technol, 2016, 34(3): 178 DOI: 10.3969/j.issn.1001-3784.2016.03.004
[4] 尤萌萌, 潘诗琰, 申小平, 等. 粉末压制过程数值模拟的研究现状及展望. 粉末冶金工业, 2017, 27(4): 49 https://www.cnki.com.cn/Article/CJFDTOTAL-FMYG201704015.htm Yu M M, Pan S Y, Shen X P, et al. Current progress and prospect of numerical simulation in powder compaction. Powder Metall Ind, 2017, 27(4): 49 https://www.cnki.com.cn/Article/CJFDTOTAL-FMYG201704015.htm
[5] 胡建华, 尚会森, 程呈, 等. 金属粉末压制成形理论与工艺进展. 热加工工艺, 2012, 41(20): 45 https://www.cnki.com.cn/Article/CJFDTOTAL-SJGY201220012.htm Hu J H, Shang H S, Cheng C, et al. Research progress of metal powder compression theory and technology. Hot Working Technol, 2012, 41(20): 45 https://www.cnki.com.cn/Article/CJFDTOTAL-SJGY201220012.htm
[6] 孙婧, 何佩珊, 齐梦菊. 关于颗粒流软件PFC的离散元数值模拟参数标定. 山东工业技术, 2016(10): 42 https://www.cnki.com.cn/Article/CJFDTOTAL-SDGJ201610040.htm Sun J, He P S, Qi M J. Parameter calibration of discrete element numerical simulation by particle flow PFC software. Shandong Ind Technol, 2016(10): 42 https://www.cnki.com.cn/Article/CJFDTOTAL-SDGJ201610040.htm
[7] 徐泳, 孙其诚, 张凌, 等. 颗粒离散元法研究进展. 力学进展, 2003, 33(2): 251 DOI: 10.3321/j.issn:1000-0992.2003.02.010 Xu Y, Sun Q C, Zhang L, et al. Advances in discrete element methods for particulate materials. Adv Mech, 2003, 33(2): 251 DOI: 10.3321/j.issn:1000-0992.2003.02.010
[8] 程远方, 果世驹, 赖和怡. 球形颗粒随机排列过程的计算机模拟. 北京科技大学学报, 1999, 21(4): 387 DOI: 10.3321/j.issn:1001-053X.1999.04.020 Cheng Y F, Guo S J, Lai H Y. Computer simulation of random packing of spherical particles. J Univ Sci Technol Beijing, 1999, 21(4): 387 DOI: 10.3321/j.issn:1001-053X.1999.04.020
[9] 郑洲顺, 朱远鹏, 裴朝旭, 等. 高速压制成形中应力波传播的特征. 系统仿真学报, 2009, 21(增刊2): 226 https://www.cnki.com.cn/Article/CJFDTOTAL-XTFZ2009S2060.htm Zheng Z S, Zhu Y P, Pei Z X, et al. Characteristics of stress wave propagation in high velocity compaction. J Syst Simul, 2009, 21(Supple 2): 226 https://www.cnki.com.cn/Article/CJFDTOTAL-XTFZ2009S2060.htm
[10] 杜欣, 曾亚武, 高睿, 等. 用离散元方法研究颗粒外形对摩擦机理的影响. 西南交通大学学报, 2012, 47(2): 252 https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT201202015.htm Du X, Ceng Y W, Gao R, et al. Effects of particle shape on friction mechanism based on discrete element method. J Southwest Jiao Tong Univ, 2012, 47(2): 252 https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT201202015.htm
[11] 曹秒艳, 董国疆, 赵长财. 基于离散元法的固体颗粒介质传力特性研究. 机械工程学报, 2011, 47(14): 62 https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB201114012.htm Cao M Y, Dong G J, Zhao C C. Research on pressure-transfer characteristics in the solid granule medium forming based on the discrete element method. J Mech Eng, 2011, 47(14): 62 https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB201114012.htm
[12] 易明军, 尹海清, 曲选辉, 等. 力与应力波对高速压制压坯质量的影响. 粉末冶金技术, 2009, 27(3): 207 http://pmt.ustb.edu.cn/article/id/fmyjjs200903012 Yi M J, Yin H Q, Qu X H, et al. Influence of force and stress wave on the quality of green compacts in high velocity compaction. Powder Metall Technol, 2009, 27(3): 207 http://pmt.ustb.edu.cn/article/id/fmyjjs200903012
[13] Huang Z M, Ma Z G, Zhang L, et al. A numerical study of macro-mesoscopic mechanical properties of gangue backfill under biaxial compression. Int J Min Sci Technol, 2016, 26(2): 309 DOI: 10.1016/j.ijmst.2015.12.018
[14] 张炜, 周剑, 于世伟, 等. 离散元法金属粉末高速压制过程中力链特性量化研究. 机械工程学报, 2018, 54(10): 85 https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB201810012.htm Zhang W, Zhou J, Yu S W, et al. Quantitative investigation on force chains of metal powder in high velocity compaction by using discrete element method. J Mech Eng, 2018, 54(10): 85 https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB201810012.htm
[15] 孙其诚, 王光谦. 静态堆积颗粒中的力链分布. 物理学报, 2008, 57(8): 4667 DOI: 10.3321/j.issn:1000-3290.2008.08.007 Sun Q C, Wang G Q. Force distribution in static granular matter in two dimensions. Acta Phys Sin, 2008, 57(8): 4667 DOI: 10.3321/j.issn:1000-3290.2008.08.007
-
期刊类型引用(9)
1. 陈新宇，李奋强，蒋继帅. 数值模拟在粉末压制细观分析中的应用与发展. 粉末冶金技术. 2024(04): 418-426 . 
本站查看
2. 张炜，萧伟健，袁传牛，张宁，陈荣昕. 基于三维离散元模型粉末压制中力链对阻塞行为的影响机制. 粉末冶金技术. 2024(04): 403-410+417 . 本站查看
3. 李化蓥，刘军，张超，张璐栋，王海陆，柯建忠. 基于离散元锥形零件冲击加载的相对密度. 粉末冶金技术. 2023(04): 322-329 . 本站查看
4. 王树强，陈钊，陈昊雷，周游. 机械镀锌过程中锌粉运动的模拟分析. 电镀与涂饰. 2022(01): 23-27 . 百度学术
5. 张炜，谈健君，张帅，陈荣昕，陈丙三，张宁，刘焜. 基于颗粒物质力学的铁粉末压制中摩擦特性对力链演化影响. 摩擦学学报. 2022(02): 386-395 . 百度学术
6. 薛亚军，贺福强，陈发江，徐浩然. 基于离散元法的木质板材压制成形过程仿真与分析. 林业机械与木工设备. 2021(05): 52-57 . 百度学术
7. 王海陆，刘军，林立，张超，张璐栋，柯建忠，李化蓥. 基于离散元的不同粒径配比粉末压制相对密度与力链分析. 粉末冶金技术. 2021(06): 490-498 . 本站查看
8. 刘义伦，曾洋. 不同成型工艺下钕铁硼模压成型过程的力学行为分析. 粉末冶金技术. 2020(04): 262-268 . 本站查看
9. 张璐栋，刘军，罗晓龙，张超，林立，周纯，王海陆. 基于离散元法的颗粒高速压制模拟及动态力学分析. 粉末冶金技术. 2020(05): 350-356+362 . 本站查看
其他类型引用(5)
计量
- 文章访问数: 421
- HTML全文浏览量: 114
- PDF下载量: 41
- 被引次数: 14
